Answer:
The distance is

Step-by-step explanation:
From the question we are told that
The period of the moon
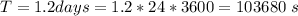
The mass of the planet is
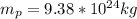
Generally the period of the moon is mathematically represented as
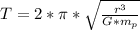
Here G is the gravitational constant with value
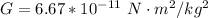
=>
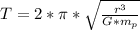
=>

=>

=>
![r = \sqrt[3]{ 1.7031241*10^(23)}](https://img.qammunity.org/2021/formulas/physics/college/ygvy4zup3u7494vkltyrul1wlqwcyt7pbv.png) j
j
=>
