Question

Find the sum of the first 47 terms of the following series, to the nearest integer.

13, 18, 23, ...

Answer 1

The sum of the first 47 terms of the given series = 6016

Explanation:

Given the sequence

13, 18, 23, ...

An arithmetic sequence has a constant difference 'd' and is defined by

`a_n=a_1+\left(n-1\right)d`

`18-13=5,\:\quad \:23-18=5`

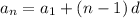
As the difference between all the adjacent terms is the same.

so

`d=5`

`a_1=13`

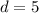
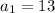
Arithmetic sequence sum formula

`n\left(a_1+(d\left(n-1\right))/(2)\right)`

Put the values

`d=5`

`a_1=13`

`n=47`

`=47\left(13+(5\left(47-1\right))/(2)\right)`

`=47\left(13+(5\left(47-1\right))/(2)\right)`

`=47\left(13+115\right)`

`=47\cdot \:128`

`=6016`

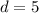
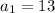
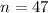
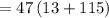
Thus, the sum of the first 47 terms of the given series = 6016