Question

Solving a compound inequality. check all that apply.

Answer 1

The solutions are:

-28.25, -14.5, -2.25

Explanation:

Given compound inequality is:

`-17.5\leq (2x+4)/(3) <17.5`

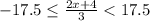
The compound inequalities are broken down into two inequalities to find the solution

The two inequalities will be:

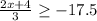`(2x+4)/(3) \geq -17.5` AND
`(2x+4)/(3)<{17.5}`

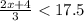
Solving both inequalities one by one

`(2x+4)/(3) \geq -17.5\\2x+4 \geq -52.5\\2x \geq -52.5-4\\2x \geq -56.5\\(2x)/(2) \geq (-56.5)/(2)\\x \geq -28.25\\(2x+4)/(3) < 17.5\\2x+4 < 52.5\\2x < 52.5-4\\2x \geq 48.5\\(2x)/(2) \geq (48.5)/(2)\\x < 24.25`

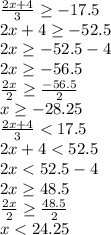
The solution is:

-28.25 ≤ x < 24.25

We have to see which options lie in the solution range.

The solutions are:

-28.25, -14.5, -2.25