Question

A line segment AB has the coordinates A (2,3) AND B ( 8,11) answer the following questions (1) What is the slope of AB? (2) What is the length of AB? (3) What are the coordinates of the mid point of AB?(4) What is the slope of a line perpendicular to AB ?

Answer 1

Given:

Endpoints of a line segment AB are A(2,3) and B(8,11).

To find:

(1) Slope of AB.

(2) Length of AB.

(3) Midpoint of AB.

(4) Slope of a line perpendicular to AB.

Solution:

We have, endpoints of line segment AB, A(2,3) and B(8,11).

(1)

Slope of AB is

`m=(y_2-y_1)/(x_2-x_1)`

`m=(11-3)/(8-2)`

`m=(8)/(6)`

`m=(4)/(3)`

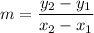
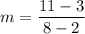
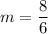
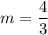
Therefore, the slope of AB is
`(4)/(3)`.

(2)

Length of AB is

`AB=√((x_2-x_1)^2+(y_2-y_1)^2)`

`AB=√((8-2)^2+(11-3)^2)`

`AB=√((6)^2+(8)^2)`

`AB=√(36+64)`

`AB=√(100)`

`AB=10`

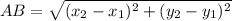
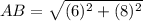
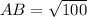
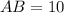
Therefore, the length of AB is 10 units.

(3) Midpoint of AB is

`Midpoint=\left((x_1+x_2)/(2),(y_1+y_2)/(2)\right)`

`Midpoint=\left((2+8)/(2),(3+11)/(2)\right)`

`Midpoint=\left((10)/(2),(14)/(2)\right)`

`Midpoint=\left(5,7\right)`

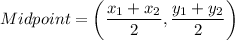
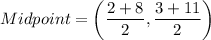
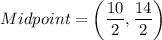
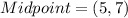
Therefore, the midpoint of AB is (5,7).

(4)

Product of slopes of two perpendicular lines is -1.

Let the slope of line perpendicular to AB be m₁.

`m_1* (4)/(3)=-1`

`m_1=-(3)/(4)`

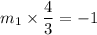
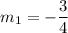
So, slope of line perpendicular to AB is
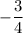`-(3)/(4)`.