Question

A merry go round exerts a force of 1000 N on a rider on the

outer ring of animals when it takes 15 seconds to make a
complete revolution. If the person weighs 750 N, the radius
of the circle he is making is m. Round your answer to
the nearest tenth.

Answer 1

The radius of the circle made by the person on the merry go round is 74.55 meters

Step-by-step explanation:

The given parameters are;

The force the merry go round exerts on the rider = 1000 N

The time it takes the merry go round to make one complete revolution = 15 seconds

The weight of the person = 750 N

The radius of the circle made by the person on the merry go round = r

We have;

`F_c = (m \cdot v^2)/(r) = m \cdot \omega ^2 \cdot r`

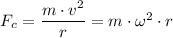
Where;

m = The mass of the person

v = The velocity of the person

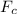`F_c` = The centrifugal force acting on the person = 1,000 N

r = The radius of the circle made by the person on the merry go round

ω = Angular velocity = 2·π/15 rad/s

We have;

The mass of the person = The weight/(The acceleration due to gravity, g)

∴ The mass of the person = 750/9.81 ≈ 76.45 kg

By substituting the calculated and known values into the equation for the centripetal force, we have;

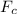`F_c` = m × ω² × r

1000 = 76.45 × (2·π/15)² × r

r = 1000/(76.45 × (2·π/15)²) = 74.55 m

The radius of the circle made by the person on the merry go round = r = 74.55 m.