Question

Desde un rascacielos de 300 m de altura se lanza un objeto con una velocidad inicial de 50 m/s. Calcula el tiempo que transcurre hasta que llega al suelo y con qué velocidad llega en cada uno de los casos: a) Si se lanza verticalmente hacia arriba. b) Si se lanza verticalmente hacia abajo. c) Si se lanza horizontalmente (En este caso calcular también la distancia al edificio cuando llega al suelo) d) Si se lanza con un ángulo de 30o (Calcular también distancia al edificio)

Answer 1

a) t = 14.2 s , v = -92 m / s , b) v = - 59.16 m / s , t = 0.916 s

c) t = 7.75 s , x = 387.5 m

d) t = 10.64 s , x = 463.9 m , v = 92.2 m / s

Step-by-step explanation:

This is an exercise in kinematics, suppose we take the upward direction as positive

a) is thrown up vertically.

Let's use the equation

y = y₀ + v₀ t - ½ g t²

When reaching the ground y = 0, the initial height is y₀ = 300 m and the initial velocity is v₀ = + 50m / s, to simplify we use g = 10 m /s² as the value of the acceleration of gravity, for a more exact calculation we can must use 9.80 m /s²

0 = y₀ + v₀t - ½ g t²

½ 10 t² - 50 t - 300 = 0

Let's solve the quadratic equation

t² - 10 t - 60 = 0

t = [10 ±√ (10² + 4 60)] / 2

t = [10 ± 18.4] / 2

t₁ = 14.2 s

t₂ = -4.2 s

since time must be a positive quantity, the correctors result t = 14.2 s

the speed at this point is

v = v₀ - g t

v = 50 - 10 14.2

v = -92 m / s

the sign indicates that the body is going down

b) in this case the initial velocity is vo = -50 m / s

let's calculate the velocity on the ground

v² = v₀² - 2g (y-y₀)

v² = 50 2 - 2 10 ((0- 300)

v² = 3500

v = + - 59.16 m / s

as the body is going down the correct sign is the negative

v = - 59.16 m / s

the time it takes to arrive is

v = v₀ - g t

t = (v₀ - v) / g

t = (-50 + 59.16) / 10

t = 0.916 s

c) the velocity is horizontal (vox = 50 m / s), this implies that the vertical velocity is zero voy = 0

y = y₀ + v₀ t - ½ g t²

0 = 300 + 0 - ½ 10 t²

t = √ (2 300/10)

t = 7.75 s

the horizontal displacement at this time is

x = v₀ₓ t

x = 50 7.75

x = 387.5 m

d) as it is thrown with an angle let's find each component of the velocities

v₀ₓ = v₀ cos 30

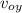`v_(oy)` = v₀ sin 30

v₀ₓ = 50 cos 30 = 43.3 m / s

v_{oy} = 50 sin 30 = 25 m / s

we look for the time of descent

y = y₀ + v_{oy} t - ½ g t²

0 = y₀ + v_{oy} t - ½ g t²

0 = 300 + 25 t - ½ 10 t²

t² - 5t - 60 = 0

we solve the second degree equation

t = [5 ±√ (5² + 4 60)] / 2

t = [5 ± 16.28] / 2

t₁ = 10.64 s

t₂ = -5.64 s

since the time must be positive the result is t = 10.64 s

the range on the x axis is

x = v₀ₓ t

x = 43.6 10.64

x = 463.9 m

the ground speed is

v_{y} =
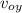`v_(oy)` - g t

v_{y} = 25 - 10 10.64

v_{y} = -81.4 m / s

speed is

v = √ (v₀ₓ² + v_{y}²)

v = √ (43.3² + 81.4²)

v = 92.2 m / s