Question

An angle measures 20° less than the measure of its complementary angle. What is the measure of each angle

Answer 1

The angle measure is 35°.

Explanation:

Complementary angles in geometry are angles that summate to exactly 90 degrees. If an angle measures 20 degrees less than the measure of its complementary angle, we can create an equation to find the measure of this angle.

The complementary angle is going to equal 90 - x, so this becomes a term in our equation: (90 - x)

Both angles need to add up to 90 degrees, so we can set up this equation:

x = (90 - x) - 20, where x is our unknown angle.

Now, we can just solve for x.

`x = (90-x)-20\\\\x = 90 - x - 20\\\\x = 70 - x \\\\2x = 70\\\\\bold{x = 35}`

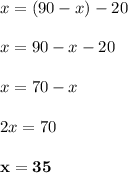
Therefore, the angle that measures 20 degrees less than its complementary angle is 35°. We can check this by using substitution:

`90 = x + 35\\\\55 = x \rightarrow x = 55\\\\55 - 35 = 20`

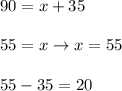
Therefore, the two angles are 55° and 35°, but the angle that measures 20° less than the measure of its complementary angle is 35°.