Answer:
The minimum sample required = 1296.65
Explanation:
Given that:
Variance
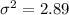
Standard deviation
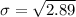
Standard deviation

Margin of error = 0.11
Confidence Interval = 98%
Level of significance = 1 - 0.98 = 0.02
The critical value =
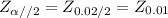
= 2.33
Thus, the minimum sample size is given by the formula:

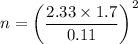
n = 1296.65