Question

Two rectangular prisms are similar. The ratio of the areas of the bases is 121:49. What is the ratio of the volumes of the similar solids?

Answer 1

The ratio of the volumes of the similar solids is 1331:343.

Explanation:

Ratios

Given the ratio of two lengths is a:b. Given a two-dimensional shape is similar to another shape, the ratio of their areas is
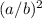`(a/b)^2`, and the ratio of their volumes is
`(a/b)^3`.

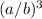We know the ratio of the areas of the bases of two similar rectangular prisms is 121:49. Thus, the ratio of its dimensions is:

`(a/b)^2=(121/49)`

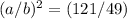
Taking the square root:

`a/b = √(121/49)=11/7`

Thus, the ratio of the volumes is:

`(a/b)^3=(11/7)^3=1331/343`

The ratio of the volumes of the similar solids is 1331:343.