Question

Find three positive consecutive odd integers such that the square of the middle integer increased by 4 times the largest integer is 173

Answer 1

9, 11, 13.

Explanation:

Let the first positive odd integer be x.

Hence, the three consecutive odd integers will be x, (x + 2), and (x + 4).

The square of the middle integer increased by four times the largest integer is 173. In other words:

`\displaystyle (x+2)^2 + 4(x+4) = 173`

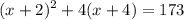
Solve for x:

`\displaystyle \begin{aligned} (x^2+4x+4) + (4x+16) & = 173 \\ \\ x^2 + 8x + 20 & = 173 \\ \\ x^2 + 8x - 153 & =0 \\ \\ (x+17)(x-9)& = 0 \\ \\ x +17 = 0 \text{ or } x-9&= 0 \\ \\ x = -17 \text{ or } x & = 9\end{aligned}`

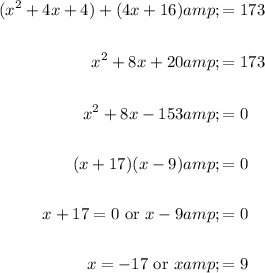
Because the integers must be positive, we can ignore the first solution.

In conclusion, our three consecutive odd integers are 9, 11, 13.