Answer:
Complete ionic:
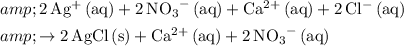 .
.
Net ionic:
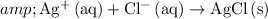 .
.
Step-by-step explanation:
Start by identifying species that exist as ions. In general, such species include:
- Soluble salts.
- Strong acids and strong bases.
All four species in this particular question are salts. However, only three of them are generally soluble in water:
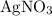 ,
,
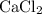 , and
, and
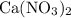 . These three salts will exist as ions:
. These three salts will exist as ions:
- Each
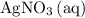 formula unit will exist as one
formula unit will exist as one
 ion and one
ion and one
 ion.
ion. - Each
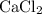 formula unit will exist as one
formula unit will exist as one
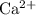 ion and two
ion and two
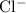 ions (note the subscript in the formula
ions (note the subscript in the formula
 .)
.) - Each
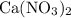 formula unit will exist as one
formula unit will exist as one
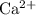 and two
and two
 ions.
ions.
On the other hand,
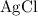 is generally insoluble in water. This salt will not form ions.
is generally insoluble in water. This salt will not form ions.
Rewrite the original chemical equation to get the corresponding ionic equation. In this question, rewrite
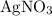 ,
,
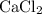 , and
, and
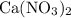 (three soluble salts) as the corresponding ions.
(three soluble salts) as the corresponding ions.
Pay attention to the coefficient of each species. For example, indeed each
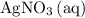 formula unit will exist as only one
formula unit will exist as only one
 ion and one
ion and one
 ion. However, because the coefficient of
ion. However, because the coefficient of
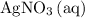 in the original equation is two,
in the original equation is two,
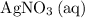 alone should correspond to two
alone should correspond to two
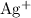 ions and two
ions and two
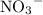 ions.
ions.
Do not rewrite the salt
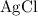 because it is insoluble.
because it is insoluble.
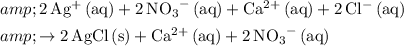 .
.
Eliminate ions that are present on both sides of this ionic equation. In this question, such ions include one unit of
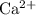 and two units of
and two units of
 . Doing so will give:
. Doing so will give:
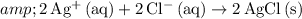 .
.
Simplify the coefficients:
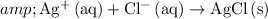 .
.