Question

Given function of f(x) = 2x - 1 and fg(x) = 10x + 3, find the function of g(x)​

Answer 1

The function of g(x) = 5x + 2

Explanation:

Let us use the composite function to solve the question

∵ f(x) = 2x - 1

∵ f(g(x)) = 10x + 3

→ f(g(x)) means substitute x in f(x) by g(x)

∴ f(g(x)) = 2[g(x)] - 1

→ Equate the two right sides of f(g(x))

∴ 2[g(x)] - 1 = 10x + 3

→ Add 1 to both sides

∴ 2[g(x)] - 1 + 1 = 10x + 3 + 1

∴ 2[g(x)] = 10x + 4

→ Divide each term into both sides by 2

∵
`(2[g(x)])/(2)` =
`(10x)/(2)` +
`(4)/(2)`

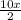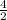
∴ g(x) = 5x + 2

∴ The function of g(x) = 5x + 2