Answer:
See Below.
Explanation:
We are given the function:
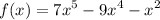
And we want to show that it has at least one zero between x = 1 and x = 2.
Because the function is a polynomial, it is everywhere continuous.
Evaluate the function at x = 1 and x = 2:
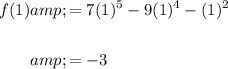
And:
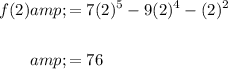
Therefore, because the function changes signs from x = 1 to x = 2 and is continuous on the interval [1, 2], by the intermediate value theorem, there must exist at least one zero in the interval.