Question

Select the sequences that are geometric.
18, 36, 54, 72,...
4.1, 8.2, 16.4, 32.8,...

Answer 1

Both sequences are geometric

Explanation:

because both have common differences of 2 times

Answer 2

4.1, 8.2, 16.4, 32.8,... is a geometric sequence.

Explanation:

Given the first sequence

18, 36, 54, 72,...

we know that the geometric sequence is the sequence that has the same common ratio 'r' (constant ratio).

Computing the ratios of all the adjacent terms:

`(36)/(18)=2,\:\quad (54)/(36)=1.5,\:\quad (72)/(54)=1.33333\dots`

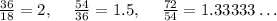
As the ratio is not constant.

Hence, 18, 36, 54, 72,... is NOT the geometric sequence.

Given the second sequence

4.1, 8.2, 16.4, 32.8,...

we know that the geometric sequence is the sequence that has the same common ratio 'r' (constant ratio).

Computing the ratios of all the adjacent terms:

`(8.2)/(4.1)=2,\:\quad (16.4)/(8.2)=2,\:\quad (32.8)/(16.4)=2`

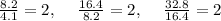
As the ratio of all the adjacent terms is the same (constant ratio).

Hence, 4.1, 8.2, 16.4, 32.8,... is a geometric sequence.

Therefore, 4.1, 8.2, 16.4, 32.8,... is a geometric sequence.