Question

In the arithmetic sequence 5,2,-1,-4 what term is -25?

Answer 1

Thus, the eleventh term is -25.

Explanation:

Arithmetic Sequences

The arithmetic sequences are identified because any term n is obtained by adding or subtracting a fixed number to the previous term. That number is called the common difference.

The equation to calculate the nth term of an arithmetic sequence is:

`a_n=a_1+(n-1)r`

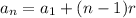
Where

an = nth term

a1 = first term

r = common difference

n = number of the term

We are given the sequence:

5,2,-1,-4,...

We can directly find the common difference by subtracting two successive terms:

r = 2 - 5 = -3

The same result is obtained by subtracting any pair of successive terms.

The first term is a1 = 5. The general equation is:

`a_n=5-3(n-1)`

`a_n=5-3n+3`

`a_n=-3n+8`

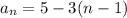
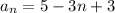
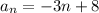
We need to find which term is -25, thus:

-3n + 8 = -25

Subtracting 8:

-3n = -25 - 8 = -33

Dividing by -3:

n = -33 / (-3)

n = 11

Thus, the eleventh term is -25.