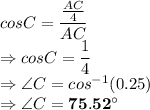Question

If a 30 foot ladder is positioned so that the bottom of the ladder is 1/4 of its length away from the wall, what angle does the ladder make with the ground

Answer 1

`75.52^\circ`

Explanation:

Given that:

The length of the ladder = 30 ft

Distance between bottom of ladder and wall =
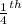`(1)/(4)^(th)` of its length

To find:

Angle made between the ladder and ground = ?

Solution:

This situation can be compared with a right angled
`\triangle ABC` as shown in the attached image in the answer area.

Side AC being the hypotenuse has the ladder along it.

AB is the wall.

BC is the distance between the wall and foot of ladder.

Formula for cosine trigonometric ratio:

`cos\theta = (Base)/(Hypotenuse)`

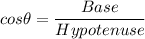
In
`\triangle ABC`:

`cosC=(BC)/(AC)`

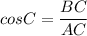
Putting the values:

`BC=(AC)/(4)`

`cosC=\frac{\frac{AC}4}{AC}\\\Rightarrow cos C = (1)/(4)\\\Rightarrow \angle C = cos^(-1)(0.25)\\\Rightarrow \angle C =\bold{75.52^\circ}`