Answer:
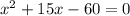
The actual dimension is 18.28 by 3.28
Explanation:
Given
Dimension:
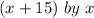
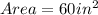
Required
Determine the quadratic equation and get the possible values of x
Solving (a): Quadratic Equation.
The cardboard is rectangular in shape.
Hence, Area is calculated as thus:
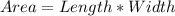
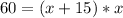
Open Bracket

Subtract 60 from both sides
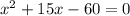
Hence, the above represents the quadratic equation
Solving (b): The actual dimension
First, we need to solve for x
This can be solved using quadratic formula:
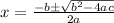
Where
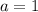
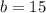
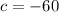
So:
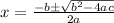

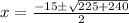
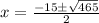
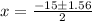
Split:
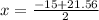 or
or
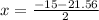
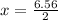 or
or

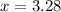 or
or
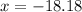
But length can't be negative;
So:
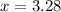
The actual dimensions:
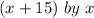 is
is
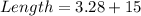
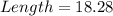
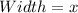

The actual dimension is 18.28 by 3.28