Question

Isabel is pulling water up from an old-fashioned well. She lifts the bucket of water at a rate of 4 ft/s, and after 1 s, the bucket is 1 ft below the top of the well. What is the equation in point-slope form of the line that represents the height of the bucket relative to the top of the well?

Answer 1

The equation in point-slope form of the line that represents the height of the bucket relative to the top of the well is
`y + 1 = 4\cdot (t-1)`.

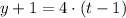Explanation:

The point-slope form of the equation of the line is represented by the following expression:

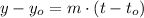`y - y_(o) = m\cdot (t-t_(o))` (1)

Where:

`t` - Time, measured in seconds.

`y` - Height below the top of the well, measured in feet.

`t_(o)`,
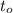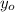`y_(o)` - Known information of the well, measured in seconds and feet, respectively.

`m` - Slope, measured in feet per second.

If we know that
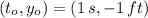`(t_(o),y_(o)) = \left( 1\,s, -1\,ft\right)` and
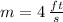`m = 4\,(ft)/(s)`, then the equation in point-slope form of the line is:

`y + 1 = 4\cdot (t-1)`

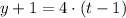
The equation in point-slope form of the line that represents the height of the bucket relative to the top of the well is
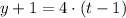`y + 1 = 4\cdot (t-1)`.