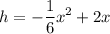Answer:
Explanation:
We are given that the height of the tunnel is modeled by:
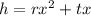
Where r and t are constants.
We are also given that the maximum height of the tunnel h is six meters.
And at ground level, the width is 12 meters.
And we want to determine the equation of the parabola.
First, since this is a quadratic, our maximum height h will occur at the vertex of our equation.
Recall that the vertex is given by the formulas:
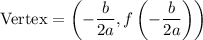
In our case, we have the function:
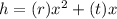
Hence, a = r; b = t; and c = 0.
Therefore, the x-coordinate of our vertex is:
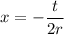
Therefore, if we substitute this back into our equation, the result should be six since six is the maximum height. Hence:
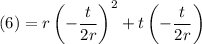
Simplify:
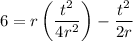
Simplify:
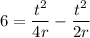
Subtract:
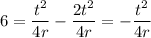
Multiply:
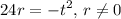
Solve for r:
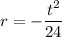
Next, we are given that the width is 12 meters at ground level.
Hence, when h = 0, the difference of our roots is 12:
We have:
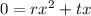
Factor:
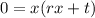
By the Zero Product Property:
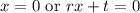
Hence, the first zero is 0.
Therefore, the second zero must be 12 to ensure that our width is 12.
Let's isolate the second zero. Subtract t from both sides:

Divide both sides by r:
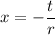
We know that this zero must be 12. Thus:
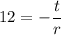
We have previously solved for r. Substitute:
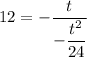
Simplify:
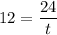
Take the reciprocal of both sides:
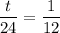
Multiply. Hence, the value of t is:
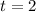
Find r. Recall that:
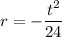
Therefore:
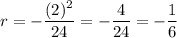
Then in conclusion, our equation will be: