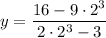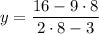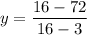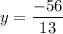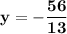Question

Need help with my homework ​

Answer 1

`\displaystyle y=(16-9x^3)/(2x^3 - 3)`

`\displaystyle y=-(56)/(13)`

Explanation:

Equation Solving

We are given the equation:

`\displaystyle x=\sqrt[3]{(3y+16)/(2y+9)}`

i)

To make y as a subject, we need to isolate y, that is, leaving it alone in the left side of the equation, and an expression with no y's to the right side.

We have to make it in steps like follows.

Cube both sides:

`\displaystyle x^3=\left(\sqrt[3]{(3y+16)/(2y+9)}\right)^3`

Simplify the radical with the cube:

`\displaystyle x^3=(3y+16)/(2y+9)`

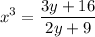
Multiply by 2y+9

`\displaystyle x^3(2y+9)=(3y+16)/(2y+9)(2y+9)`

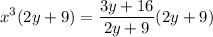
Simplify:

`\displaystyle x^3(2y+9)=3y+16`

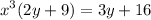
Operate the parentheses:

`\displaystyle x^3(2y)+x^3(9)=3y+16`

`\displaystyle 2x^3y+9x^3=3y+16`

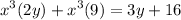
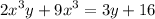
Subtract 3y and
`9x^3`:

`\displaystyle 2x^3y - 3y=16-9x^3`

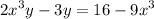
Factor y out of the left side:

`\displaystyle y(2x^3 - 3)=16-9x^3`

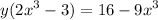
Divide by
`2x^3 - 3`:

`\mathbf{\displaystyle y=(16-9x^3)/(2x^3 - 3)}`

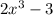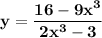
ii) To find y when x=2, substitute:

`\displaystyle y=(16-9\cdot 2^3)/(2\cdot 2^3 - 3)`

`\displaystyle y=(16-9\cdot 8)/(2\cdot 8 - 3)`

`\displaystyle y=(16-72)/(16- 3)`

`\displaystyle y=(-56)/(13)`

`\mathbf{\displaystyle y=-(56)/(13)}`