Question

Prove algebraically that n^2 -n is never an odd number when n>1

Answer 1

See Below.

Explanation:

We want to prove that:

`n^2-n`

Is never an odd number when n>1.

We will have two cases. We can prove them for each case individually.

The Even Case: n is Even:

Let n be even. Then, we can rewrite n as:

`n=2k`

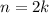
Where k is any positive integer.

This is because twice of any integer is even, so n must be even.

Substitute this into our expression to acquire:

`=(2k)^2-(2k)`

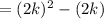
Square:

`=4k^2-2k`

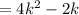
4 times anything is even. 2 times anything is also even. Therefore, our expression will stay even.

The Odd Case: n is Odd:

Let n be odd. Then we can rewrite n as:

`n=2k-1`

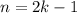
Where k is any positive integer.

This is odd because twice of any number is even, but if subtracted by 1, it yields an odd number.

We will substitute this into our expression to acquire:

`=(2k-1)^2-(2k-1)`

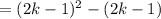
Square:

`=(4k^2-4k+1)+(-2k+1)`

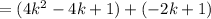
Simplify:

`=4k^2-6k+2`

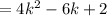
4 times anything is even. 6 times anything is even. And anything even added to 2 will still be even.

Therefore:

`n^2-n`

Will never be an odd number when n>1.