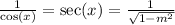It given that sin(-x) = -m where x is acute angle . express sec x in terms of m

Question

asked May 6, 2021 135k views

1 Answer

DrXCheng · Answer 1 · 2021-05-12T04:44:22+0000

Answer:

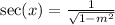
$\sec(x)=(1)/(√(1-m^2))$

Explanation:

We know that:

$\sin(-x)=-m$

First, since sine is an odd function, we can move the negative outside:

$=-\sin(x)=-m$

Divide both sides by -1:

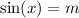
$\sin(x)=m$

We will now use the Pythagorean Identity:

$\cos^2(x)+\sin^2(x)=1$

Substitute m for sine:

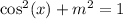
$\cos^2(x)+m^2=1$

Solve for cosine:

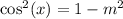
$\cos^2(x)=1-m^2$

Take the square root of both sides:

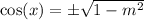
$\cos(x)=\pm√(1-m^2)$

Since x is an acute angle, cosine will always be positive. Thus:

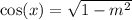
$\cos(x)=√(1-m^2)$

Take the reciprocal of both sides. Hence:

$(1)/(\cos(x))=\sec(x)=(1)/(√(1-m^2))$