Question

If cosθ=3/5, find tanθ

Answer 1

Answer and step-by-step explanation:

cos = adj/hyp (in a right triangle)

cos0 = 3/5

adj = 3

hyp = 5

opp = sqrt( 5^2 - 3^2) = sqrt( 25-9) = sqrt(16) = 4 (Pythogorean theorem)

tan0 = opp/adj = 4/3

Answer 2

`\boxed {\boxed {\sf tan( \theta)=4/3}}`

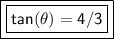
Explanation:

Cosine is equal to adjacent over hypotenuse.

• cos(x)=adjacent/hypotenuse

We are given: cosθ=3/5

• Therefore, the adjacent is 3 and the hypotenuse is 5.

We want to find tanθ. Tangent is equal to opposite over adjacent.

We need to find the other leg of the triangle, which is the "opposite". Use Pythagorean Theorem.

`a^2+b^2=c^2`

The hypotenuse (c) is 5.

`a^2+b^2=5^2`

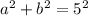
One leg (a) is 3, the other (b) is unknown.

`3^2+b^2=5^2`

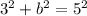
Evaluate all the exponents.

`9+b^2=25`

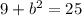
Subtract 9 from both sides of the equation.

`9-9+b^2=25-9`

`b^2=16`

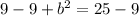
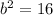
Take the square root of both sides.

`√(b^2) =√(16)`

`b=4`

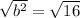
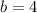
Now we know the "opposite" is 4. We can find the tangent now.

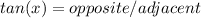`tan(x)=opposite/adjacent` (opposite=4, adjacent=3)

`tan( \theta)=4/3`

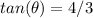
The tangent of theta is 4/3