Question

A quadratic function has an axis of symmetry at x=4 and contains the points (2, -6) and (7, -11). Find the equation in standard form (y=ax2+bx+c). Then state the "a" value in the equation.

Answer 1

The equation in standard form is
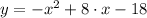`y = -x^(2)+8\cdot x -18`. The "a" value is -1.

Explanation:

A quadratic function is the standard form of the parabola. We can take advantage of the symmetry property of the parabola by using the following formula from the Analytical Geometry:

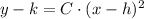`y - k = C\cdot (x-h)^(2)` (1)

Where:

`C` - Parabola constant, dimensionless.

`x` - Independent variable, dimensionless.

`y` - Depedent variable, dimensionless.

`h`,
`k` - Coordinates of the vertex of the parabola, dimensionless.

If we know that
`(x_(1),y_(1))=(2,-6)`,
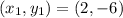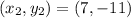`(x_(2),y_(2))=(7,-11)` and
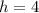`h = 4`, then we have the following system of linear equations:

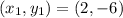
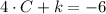`(x_(1),y_(1))=(2,-6)`

`-6-k = C\cdot (2-4)^(2)`

`4\cdot C +k = -6` (2)

`(x_(2),y_(2))=(7,-11)`

`-11-k =C\cdot (7-4)^(2)`

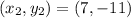
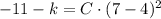
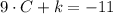`9\cdot C + k = -11` (3)

By clearing
`k` in (2) and (3) and equalizing each other, we get that:

`-6-4\cdot C = -11-9\cdot C`

`5\cdot C = -5`

`C = -1`

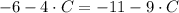
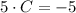
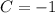
And the remaining variable is calculated by substituting directly on (3):

`k = -11-9\cdot C`

`k = -11-9\cdot (-1)`

`k = -2`

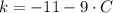
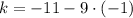
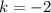
Then, the equation of the parabola is:

`y+2 = -(x-4)^(2)`

And the standard form of the equation is obtained by algebraic handling:

`y+2 = -(x^(2)-8\cdot x + 16)`

`y + 2 = -x^(2)+8\cdot x -16`

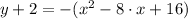
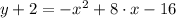
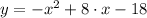`y = -x^(2)+8\cdot x -18` (4)

The equation in standard form is
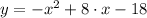`y = -x^(2)+8\cdot x -18`. The "a" value is -1.