Answer:
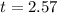
Explanation:
Given

Required
Determine the time to hit the ground
The ground is at point 0.
So, to solve this; we simply set
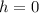 , then calculate the value of t
, then calculate the value of t
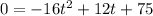
Multiply through by -1
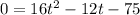
Reorder

Solve using quadratic formula:

Where

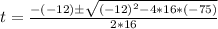
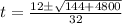
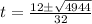
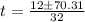
Split:
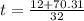 or
or
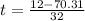
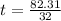 or
or
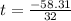
But time (t) can't be negative;
So, we make use of only
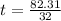
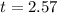
Hence, the time to hit the ground is 2.57 seconds