Question

The maximum speed possible on a length of railroad track is directly proportional to the cube root of the amount of money spent ob maintaining the track. Suppose that a maximum speed of 25 km/hr is possible on a stretch for which 450,000 was spend on maintence, find the maximum speed if the amount spent on maintence is increased to $1,750,000 Pls help me show steps please

Answer 1

`39.29\ \text{km/h}`

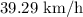
Explanation:

s = Speed of the train

m = Money spent on maintanence

`s\propto m^{(1)/(3)}`

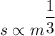
Let k be the constant of proportionality so

`s=k (m)^{(1)/(3)}`

Now a case is given where 25 km/hr is possible on a stretch for which 450,000 is spent so

s = 25

m = 450000

`s=k (m)^{(1)/(3)}\\\Rightarrow k=\frac{s}{m^{(1)/(3)}}\\\Rightarrow k=\frac{25}{450000^{(1)/(3)}}\\\Rightarrow k=0.326`

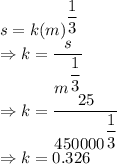
Now when m = 1750000

`s=k (m)^{(1)/(3)}\\\Rightarrow s=0.326* 1750000^{(1)/(3)}\\\Rightarrow s=39.29\ \text{km/h}`

The maximum speed of the train would be
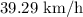`39.29\ \text{km/h}`.