Question

Which ordered pairs are solutions to the inequality y - 3x < -8?

Select each correct answer.
(1, -5)
(-3, - 2)
(0, -9)
(2, -1)
(5, 4)​

Answer 1

The ordered pairs which are solution to given inequality are:

(0,-9)

(5,4)

Explanation:

In order to check if the given ordered pairs are solution of the inequality or not we will put the ordered pairs one by one in the inequality.

If the inequality is holds true for the ordered pair, the ordered pair is the solution.

The inequality is:

`y - 3x < -8`

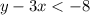
So,

For (1,-5):

`y - 3x < -8\\-5-3(1) < -8\\-5-3<-8\\-8<-8`

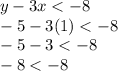
(1,-5) is not the solution of given inequality.

For (-3,-2):

`-2 - 3(-3) < -8\\-2+9<-8\\7<-8`

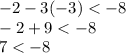
(-3,-2) is not the solution of given inequality.

For (0,-9):

`y - 3x < -8\\-9-3(0) < -8\\-9 <-8`

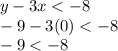
(0,-9) is the solution of the given inequality.

For (2,-1):

`y - 3x < -8`

`-1 - 3(2) < -8\\-1-3<-8\\-4<-8`

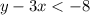
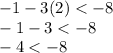
(2,-1) is not the solution of given inequality

For (5,4):

`y - 3x < -8\\4 - 3(5) < -8\\4-15<-8\\-11<-8`

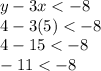
(5,4) is the solution of given inequality.

Hence,

The ordered pairs which are solution to given inequality are:

(0,-9)

(5,4)