Question

the graph of the function f(x) = (x +2)(x + 6) is shown below. On a coordinate plane, a parabola opens up. It goes through (negative 6, 0), has a vertex at (negative 4, negative 4), and goes through (negative 2, 0). What is true about the domain and range of the function? The domain is all real numbers, and the range is all real numbers greater than or equal to –4. The domain is all real numbers greater than or equal to –4, and the range is all real numbers. The domain is all real numbers such that –6 ≤ x ≤ –2, and the range is all real numbers greater than or equal to –4. The domain is all real numbers greater than or equal to –4, and the range is all real numbers such that –6 ≤ x ≤ –2.

Answer 1

b

Step-by-step explanation:

Answer 2

Answer: Choice A

Domain = all real numbers

Range = real numbers greater than or equal to -4

=====================================================

Step-by-step explanation:

The domain is the set of allowed x inputs of a function.

We can replace x with any number we want to get some output for y = f(x)

This tells us the domain is the set of all real numbers.

-----------

The range is the set of numbers y such that
`y \ge -4`

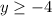
In other words, we can have y = -4 or y > -4

This is because y = -4 is the lowest output possible, as indicated by the vertex point.