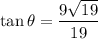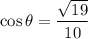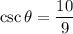Question

Find cos , csc 0, and tan 0, where is the angle shown in the figure.

Give exact values, not decimal approximations.
cose
10
9
csc
tan

Answer 1

Explanation:

Trigonometric Ratios

The ratios of the sides of a right triangle are called trigonometric ratios. There are six trigonometric ratios, sine (sin), cosine (cos), tangent (tan), cosecant (csc), secant (sec), and cotangent (cot).

The ratios are valid only in right triangles, or when one of the internal angles is 90°.

Take any of the acute angles as a reference, and the largest side as the hypotenuse, then:

`\displaystyle \cos\theta=\frac{\text{adjacent leg}}{\text{hypotenuse}}`

`\displaystyle csc\theta=\frac{\text{hypotenuse}}{\text{opposite leg}}`

`\displaystyle \tan\theta=\frac{\text{opposite leg}}{\text{adjacent leg}}`

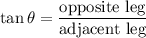
The missing side of the triangle x can be calculated by using Pythagora's Theorem:

`10^2=9^2+x^2`

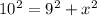
Solving:

`x^2=10^2-9^2=100-81=19`

`x=√(19)`

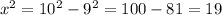
For the angle marked as θ:

`\displaystyle \tan\theta=\frac{\text{opposite leg}}{\text{adjacent leg}}`

`\displaystyle \tan\theta=\frac{\text{9}}{√(19)}`

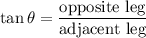
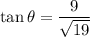
Rationalizing:

`\displaystyle \tan\theta=(9√(19))/(19)`

`\displaystyle \cos\theta=\frac{\text{adjacent leg}}{\text{hypotenuse}}`

`\displaystyle \cos\theta=(√(19) )/(10)`

`\displaystyle \csc\theta=\frac{\text{hypotenuse}}{\text{opposite leg}}`

`\displaystyle \csc\theta=(10)/(9)`