Question

In the right triangle below, an altitude is drawn to the hypotenuse. Solve
for x.

Answer 1

x = 4

Explanation:

Right Triangles

In right triangles, where one of the internal angles is 90°, the Pythagora's Theorem is satisfied:

If m is the hypotenuse of a right triangle, and p, q are the shorter sides or legs, then:

`m^2=p^2+q^2`

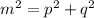
If we need to calculate any of the legs, say, p:

`p^2=m^2-q^2`

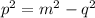
The figure below shows two additional variables z and h which will help us to find the value of x.

The triangle with sides 12, 36, z can be solved for z, being 36 the hypotenuse:

`z^2=36^2-12^2=1296-144=1152`

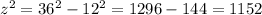
The base of the triangle to the left is (36-x), the height is h, and the hypotenuse is z, thus:

`h^2=z^2-(36-x)^2`

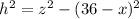
Substituting z:

`h^2=1152-(36-x)^2`

The triangle to the right has dimensions x, h, and 12, and:

`h^2=12^2-x^2`

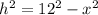
Equating both expressions for h:

`1152-(36-x)^2=12^2-x^2`

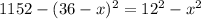
Expanding the squares:

`1152-1296+72x-x^2=144-x^2`

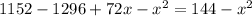
Simplifying the x squared and operating:

-144+72x=144

Adding 144:

72x = 288

Solving:

x = 288 / 72 =4

x = 4