Final answer:
The conclusions that can be drawn about
 are: it has a restricted domain, it has a y-intercept at (0, 2), and it has a maximum at (0, 2).
are: it has a restricted domain, it has a y-intercept at (0, 2), and it has a maximum at (0, 2).
Step-by-step explanation:
The function
 is a quadratic function that represents a parabola. Based on the given options, the correct conclusions that can be drawn are:
is a quadratic function that represents a parabola. Based on the given options, the correct conclusions that can be drawn are:
- f(x) has a restricted domain: The function is defined for all real numbers because there are no restrictions on the value of x.
- f(x) has an x-intercept of (2, 0): To find the x-intercept, set f(x) equal to 0 and solve for x. In this case,
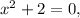 which has the solution x = ±√(-2). Since the square root of a negative number is undefined, there are no real x-intercepts, so this option is incorrect.
which has the solution x = ±√(-2). Since the square root of a negative number is undefined, there are no real x-intercepts, so this option is incorrect. - f(x) has a y-intercept at the point (0, 2): To find the y-intercept, substitute x = 0 into the function. In this case, f(0) =
 , so the y-intercept is (0, 2).
, so the y-intercept is (0, 2). - f(x) has a maximum at the point (0, 2): To determine if f(x) has a maximum or minimum, we can check the coefficient of the
 term. Since this coefficient is positive, the parabola opens upwards, and the vertex represents the maximum point. In this case, the vertex is at (0, 2).
term. Since this coefficient is positive, the parabola opens upwards, and the vertex represents the maximum point. In this case, the vertex is at (0, 2).