Question

Segment FG begins at point F(-2, 4) and ends at point G (-2, -3). Segment FG is translated by (x, y) → (x – 3, y + 2) and then reflected across the y-axis to form segment F'G'. How long is segment F'G'?

Answer 1

The length of the segment F'G' is 7.

Explanation:

From Linear Algebra we define reflection across the y-axis as follows:

`(x',y')=(-x, y)`,
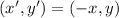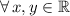`\forall\, x, y\in \mathbb{R}` (Eq. 1)

In addition, we get this translation formula from the statement of the problem:

`(x',y') =(x-3,y+2)`,
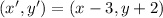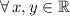`\forall \,x,y\in \mathbb{R}` (Eq. 2)

Where:

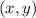`(x, y)` - Original point, dimensionless.

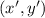`(x', y')` - Transformed point, dimensionless.

If we know that
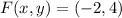`F(x,y) = (-2, 4)` and
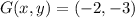`G(x,y) = (-2,-3)`, then we proceed to make all needed operations:

Translation

`F''(x,y) = (-2-3,4+2)`

`F''(x,y) = (-5,6)`

`G''(x,y) = (-2-3,-3+2)`

`G''(x,y) = (-5,-1)`

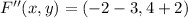
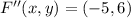
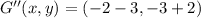
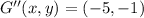
Reflection

`F'(x,y) = (5, 6)`

`G'(x,y) = (5,-1)`

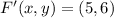
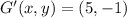
Lastly, we calculate the length of the segment F'G' by Pythagorean Theorem:

`F'G' = \sqrt{(5-5)^(2)+[(-1)-6]^(2)}`

`F'G' = 7`

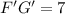
The length of the segment F'G' is 7.