Answer:
The average emf that will be induced in the wire loop during the extraction process is 37.9 V
Step-by-step explanation:
The average emf induced can be calculated from the formula
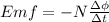
Where
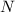 is the number of turns
is the number of turns
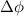 is the change in magnetic flux
is the change in magnetic flux
 is the time interval
is the time interval
The change in magnetic flux is given by

Where
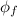 is the final magnetic flux
is the final magnetic flux
and
 is the initial magnetic flux
is the initial magnetic flux
Magnetic flux is given by the formula

Where
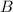 is the magnetic field
is the magnetic field
 is the area
is the area
and
 is the angle between the magnetic field and the area.
is the angle between the magnetic field and the area.
Initially, the magnetic field and the area are pointed in the same direction, that is,

From the question,
B = 1.5 T
and radius = 15.0 cm = 0.15 m
Since it is a circular loop of wire, the area is given by
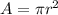
∴
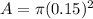
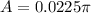
∴
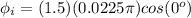
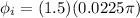
( NOTE:
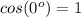 )
)
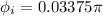 Wb
Wb
For
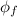
The field pointed upwards, that is
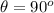 . Since
. Since
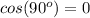
Then

Hence,
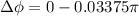
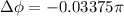
From the question

Here,
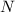 = 1
= 1
Hence,
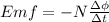 becomes
becomes
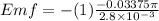

Hence, the average emf that will be induced in the wire loop during the extraction process is 37.9 V.