Answer:
Distance from point 1 = 3.2 miles
Distance from point 2 = 3.9 miles
Explanation:
Angle of elevation of the mountain at point 3 from point '1' is 78° and angle of elevation from point '2' is 53°.
m∠1 + m2 + a = 180°
53° + 78° + a° = 180°
a = 180 - 131
a = 49°
By applying Sine rule in the given triangle,

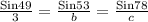
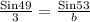
b =
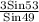 = 3.17
= 3.17
≈ 3.2 miles
Similarly,
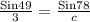
c =
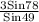
c = 3.88 ≈ 3.9 miles
Distance of the mountain from the points 1 = 3.2 miles
Distance of the mountain from the points 2 = 3.9 miles