Question

A construction zone on a highway has a posted speed limit of miles per hour. The speeds of vehicles passing through this construction zone are normally distributed with a mean of miles per hour and a standard deviation of miles per hour. Find the percentage of vehicles passing through this construction zone that are exceeding the posted speed limit. Round your answer to two decimal places.

Answer 1

The percentage of vehicles passing through this construction zone that are exceeding the posted speed limit is 89.44%.

Explanation:

The complete question is:

A construction zone on a highway has a posted speed limit of 40 miles per hour. The speeds of vehicles passing through this construction zone are normally distributed with a mean of 45 miles per hour and a standard deviation of 4 miles per hour. Find the percentage of vehicles passing through this construction zone that are exceeding the posted speed limit. Round your answer to two decimal places.

Solution:

Let X represent the speed of the vehicles passing through the construction zone.

It is provided that X follows a Normal distribution with parameters μ = 45 and σ = 4.

Compute the probability that a randomly selected vehicle exceeds the posted speed limit as follows:

`P(X>40)=P((X-\mu)/(\sigma)>(40-45)/(4))`

`=P(Z>-1.25)\\\\=P(Z<1.25)\\\\=0.89435\\\\\approx 0.8944`

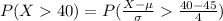
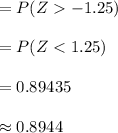
The percentage is, 0.8944 × 100 = 89.44%

Thus, the percentage of vehicles passing through this construction zone that are exceeding the posted speed limit is 89.44%.