Question

A survey is planned to estimate the proportion of voters who support a proposed gun control law. The estimate should be within a margin of error of with 99% confidence, and we do not have any prior knowledge about the proportion who might support the law. How many people need to be included in the sample

Answer 1

Complete Question

A survey is planned to estimate the proportion of voters who support a proposed gun control law. The estimate should be within a margin of error of
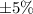`\pm 5\%` with 99 %confidence, and we do not have any prior knowledge about the proportion who might support the law. How many people need to be included in the sample?

Answer:

The value is
`n = 666`

Explanation:

From the question we are told that

The margin of error is
`E = 0.05`

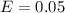
From the question we are told the confidence level is 99% , hence the level of significance is

`\alpha = (100 - 95 ) \%`

=>
`\alpha = 0.01`

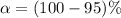
Generally from the normal distribution table the critical value of
`(\alpha )/(2)` is

`Z_{(\alpha )/(2) } = 2.58`

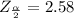
Here we will assume that the sample proportion of those who support a proposed gun control law to be
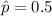`\^ p = 0.5` because from the question they do not have any prior knowledge about the proportion who might support the law

Generally the sample size is mathematically represented as

`n = [\frac{Z_{(\alpha )/(2) }}{E} ]^2 * \^ p (1 - \^ p )`

=>
`n = 666`