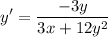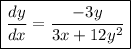Question

If 5 + 3xy + 4y^3 = 0 then find dy/dx in terms of x and y

Answer 1

`\displaystyle (dy)/(dx)=(-3y)/(3x+ 12y^2)`

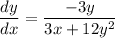
Explanation:

Implicit Differentiation

We use implicit differentiation when it's not possible to find an expression of y as a function of x, or the expression is very hard to differentiate.

The implicit differentiation takes the original equation and differentiates each term, usually applying the product, quotient, power, or other similar rules.

In the course of the differentiation, we'll use f' as the derivative of f.

We'll find y'=dy/dx in the following equation:

`5 + 3xy + 4y^3 = 0`

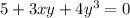
Differentiating:

`(5)' + (3xy)' + (4y^3)' = (0)'`

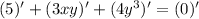
The derivative of a constant is 0, thus:

`(3xy)' + (4y^3)' = 0`

The first term is a product of variables, so we apply the product rule:

`(f.g)'=f'.g+f.g'`

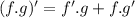
The second term is the power of y. We apply the chain rule:

`[f(g)]'=f'.g'`

`3(x'y+xy') + 4(3y^2y') = 0`

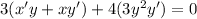
Operating:

`3x'y+3xy'+ 12y^2y' = 0`

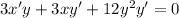
Since x'=1:

`3y+3xy'+ 12y^2y' = 0`

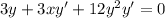
Subtracting 3y:

`3xy'+ 12y^2y' = -3y`

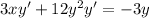
Take y' as a common factor:

`y'(3x+ 12y^2) = -3y`

Solve for y':

`\displaystyle y'=(-3y)/(3x+ 12y^2)`

`\boxed{\displaystyle (dy)/(dx)=(-3y)/(3x+ 12y^2)}`