Question

The system of equations 3x + 9y^3= -21, 13y^3+4x=-1 has exactly one solution.

Use substitution to find the solution.

What is the solution?

Enter your answer as an ordered pair, like this: (42, 53)

Answer 1

`\huge\boxed{(-88,3)}`

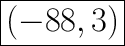
Explanation:

`\sf 3x + 9y^3 = -21` -------------------------- (1)

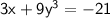`\sf 13y^3+4x= -1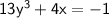` -------------------------- (2)

Multiply Eq. (1) by 13 and (2) by 9

Equation (1):

`\sf 13(3x+9y^3) = -21 * 13`

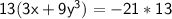
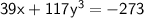`\sf 39x + 117y^3=-273` --------------------(3)

Equation (2):

`\sf 9(13y^3+4x) = -1* 9`

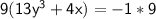
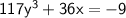`\sf 117y^3 + 36x = -9` ------------------------(4)

Subtract Eq. (2) from (1)

`\sf 39x+117y^3-117y^3 -36x=-273+9`

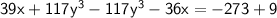
39x - 36x = -264

3x = -264

Dividing both sides by 3

x = -88

`\rule[225]{225}{2}`

Put x = -88 in Eq. (1)

3(-88)+9y³ = -21

-264 + 9y³ = -21

9y³ = -21 + 264

9y³ = 243

Dividing both sides by 9

y³ = 27

Taking cube root on both sides

y = 3

`\rule[225]{225}{2}`

Ordered Pair = (x,y) = (-88,3)

`\rule[225]{225}{2}`

Hope this helped!

~AnonymousHelper1807