Question

Write two rational numbers a/b and c/d, where a, b, c, and d are the digits 2, 3, 4, or 5, such that no digit can be used more than once and that the two rational numbers are the greatest distance apart on the number line. Explain how you got this answer.

Answer 1

Following are the solution to this question:

Explanation:

Let
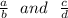`(a)/(b) \ \ and \ \ (c)/(d)` both are the rationalnumbers and for both numbers there is not a greatest distance. so, the value
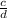`(c)/(d)` must have greatest for the value
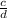`(c)/(d)` and the c is maximum and d is minimum.

if c= 5 and d=2

`\to (c)/(d) = (5)/(2)=2.5`

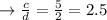
Similarly:

`\to (a)/(b)`

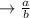
a=3 and b=4

`\to (a)/(b)=(3)/(4) = 0.75`

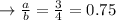
so, the
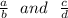`(a)/(b) \ \ and \ \ (c)/(d)` is at the great distance.