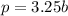Question

The equation p = 3.25b can be used to find the price, p, in dollars, of b pounds of blueberries at a particular supermarket.  Each of the tables gives the prices of various pounds of blueberries at a different supermarket.  Which of these tables represents blueberries that are more expensive than those represented by the equation?  Select all that apply.

Answer 1

Table C, Table D, Table E

Explanation:

See attachment for tables

Given

`p = 3.25b`

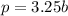
Required

Which of the tables is more expensive than the given function

To answer this question, we simply determine the equation of each table and then compare the equation with
`p = 3.25b`

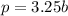
Table A:

Consider two corresponding points in the table, we have:

`(b_1,p_1) = (1,2.75)`

`(b_2,p_2) = (4,11)`

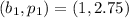
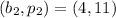
Determine the slope

`m = (p_2 - p_1)/(b_2 - b_1)`

`m = (11 - 2.75)/(4 - 1)`

`m = (8.25)/(3)`

`m = 2.75`

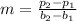
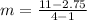
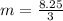
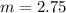
The equation is determined as follows:

`p - p_1 = m(b-b_1)`

`p - 2.75 = 2.75(b-1)`

`p - 2.75 = 2.75b-2.75`

`p = 2.75b`

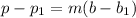
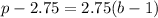
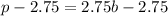
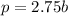
Comparing this equation to
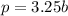`p = 3.25b`, we have that:

`2.75 < 3.25`

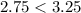
Hence:

This equation is less expensive than
`p = 3.25b`

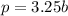
Table B:

Consider two corresponding points in the table, we have:

`(b_1,p_1) = (1.5,3.75)`

`(b_2,p_2) = (6,15)`

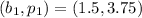
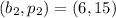
Determine the slope

`m = (p_2 - p_1)/(b_2 - b_1)`

`m = (15 - 3.75)/(6 - 1.5)`

`m = (11.25)/(4.5)`

`m = 2.5`

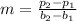
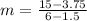
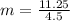
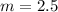
The equation is determined as follows:

`p - p_1 = m(b-b_1)`

`p - 3.75 = 2.5(b-1.5)`

`p - 3.75 = 2.5b- 3.75`

`p = 2.5b`

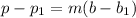
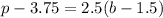
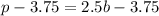
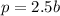
Comparing this equation to
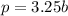`p = 3.25b`, we have that:

`2.5 < 3.25`

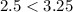
Hence:

This equation is also less expensive than
`p = 3.25b`

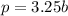
Table C:

Consider two corresponding points in the table, we have:

`(b_1,p_1) = (2,7)`

`(b_2,p_2) = (4,14)`

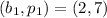
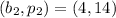
Determine the slope

`m = (p_2 - p_1)/(b_2 - b_1)`

`m = (14 - 7)/(4 - 2)`

`m = (7)/(2)`

`m = 3.5`

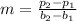
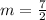
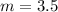
The equation is determined as follows:

`p - p_1 = m(b-b_1)`

`p - 7 = 3.5(b - 2)`

`p - 7 = 3.5b - 7`

`p = 3.5b`

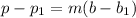
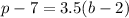
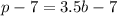
Comparing this equation to
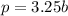`p = 3.25b`, we have that:

`3.5 > 3.25`

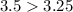
Hence:

This equation is more expensive than
`p = 3.25b`

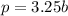
Table D:

Consider two corresponding points in the table, we have:

`(b_1,p_1) = (2.5,10)`

`(b_2,p_2) = (5,20)`

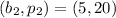
Determine the slope

`m = (p_2 - p_1)/(b_2 - b_1)`

`m = (20 - 10)/(5 - 2.5)`

`m = (10)/(2.5)`

`m = 4`

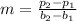
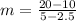
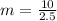
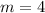
The equation is determined as follows:

`p - p_1 = m(b-b_1)`

`p - 10 = 4(b - 2.5)`

`p - 10 = 4b - 10`

`p = 4b`

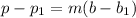
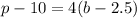
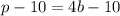
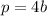
Comparing this equation to
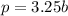`p = 3.25b`, we have that:

`4 > 3.25`

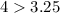
Hence:

This equation is more expensive than
`p = 3.25b`

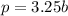
Table E:

Consider two corresponding points in the table, we have:

`(b_1,p_1) = (6, 22.5)`

`(b_2,p_2) = (12,45)`

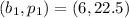
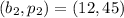
Determine the slope

`m = (p_2 - p_1)/(b_2 - b_1)`

`m = (45 - 22.5)/(12 - 6)`

`m = (22.5)/(6)`

`m = 3.75`

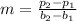
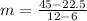
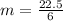
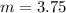
The equation is determined as follows:

`p - p_1 = m(b-b_1)`

`p - 22.5 = 3.75(b - 6)`

`p - 22.5 = 3.75b - 22.5`

`p = 3.75b`

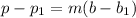
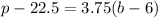
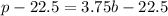
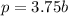
Comparing this equation to
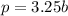`p = 3.25b`, we have that:

`3.75>3.25`

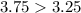
Hence:

This equation is more expensive than
`p = 3.25b`

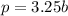
Table F:

Consider two corresponding points in the table, we have:

`(b_1,p_1) = (7, 21)`

`(b_2,p_2) = (14,42)`

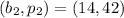
Determine the slope

`m = (p_2 - p_1)/(b_2 - b_1)`

`m = (42 - 21)/(14 - 7)`

`m = (21)/(7)`

`m = 3`

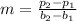
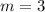
The equation is determined as follows:

`p - p_1 = m(b-b_1)`

`p -21 =3(b -7)`

`p -21 =3b -21`

`p = 3b`

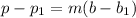
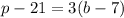
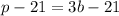
Comparing this equation to
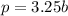`p = 3.25b`, we have that:

`3 < 3.25`

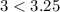
Hence:

This equation is less expensive than
`p = 3.25b`