Answer:
The function for the height of the ball in terms of its horizontal distance is
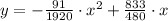
Explanation:
From Physics, we know that ball describes a parabolic motion, in which trajectory is described by the following second-order polynomial (quadratic function):
 (Eq. 1)
(Eq. 1)
Where:
 - Horizontal distance, measured in feet.
- Horizontal distance, measured in feet.
 - Vertical distance above the ground, measured in feet.
- Vertical distance above the ground, measured in feet.
 - Second order coefficient, measured in
- Second order coefficient, measured in
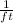 .
.
 - First order coefficient, dimensionless.
- First order coefficient, dimensionless.
 - Zero order coefficient, measured in feet.
- Zero order coefficient, measured in feet.
We can obtain the second-order polynomial associated with the soccer ball by knowing three distinct points and solving the resulting system of linear equations. If we know that
 ,
,
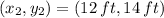 and
and
 , then the system of linear equations is:
, then the system of linear equations is:
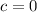
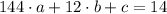
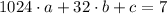
The solution of this linear system is:
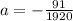 ,
,
 ,
,
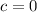
Therefore, the function for the height of the ball in terms of its horizontal distance is
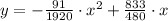
In addition, we present a graphic of the given function as attachment.