Question

The probability that a college graduate will find a full time job within three months after graduation from college is .27. Three college students, who will be graduating soon, are randomly selected. What is the probability that all three of them will find full-time jobs within three months after graduation from college

Answer 1

The probability that all three of them will find full-time jobs within three months after graduation from college is 0.0197.

Explanation:

Let X denote the number of college graduates who will find a full time job within three months after graduation from college.

A random sample of 3 college students, who will be graduating soon, are selected.

The probability of X is, p = 0.27.

Each student is independent of the other to find a full time job within three months after graduation from college.

The random variable X follows a binomial distribution with parameter n = 3 and p = 0.27.

Compute the probability that all three of them will find full-time jobs within three months after graduation from college as follows:

`P(X=3)={3\choose 3}(0.27)^(3)(-0.27)^(3-3)`

`=1* 0.019683* 1\\=0.0197`

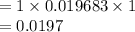
Thus, the probability that all three of them will find full-time jobs within three months after graduation from college is 0.0197.