Question

Find a polynomial function of degree 3 with real coefficients and the numbers 6, 3i as some of its zeros.

Answer 1

A polynomial function of degree 3 with real coefficients and the numbers 6 and i 3 as some of its zeroes is
`p_(3)(x) = x^(3)-6\cdot x^(2)+9\cdot x -54`.

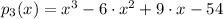Explanation:

A third-order polynomial in standard form is a sum of monomials with natural exponentials such that greatest degree of monomials is 3. This kind of polynomials is described by this definition:

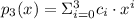`p_(3)(x) =\Sigma\limits_(i=0)^(3) c_(i) \cdot x^(i)` (Eq. 1)

Where:

`i` - Index of a sum component, dimensionless.

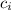`c_(i)` - i-th coefficient, dimensionless.

Where the highest value of
`i` is the degree of the polynomial.

In addition, the Fundamental Theorem establishes that all polynomials with real coefficients and degree higher than zero have a number of complex roots, an extension of the real set, equivalent to the degree of the polynomial itself.

In our case, we guarantee the existence of three complex roots, of which we know two of them:
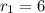`r_(1) = 6` and
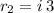`r_(2) = i\,3`. The polynomial can be represented as a product of three binomials:

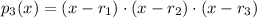`p_(3)(x) = (x-r_(1))\cdot (x-r_(2))\cdot (x-r_(3))` (Eq. 2)

Where
`r_(1)`,
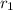`r_(2)` and
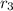`r_(3)` are the roots of the third order polynomial.

If we know that
`r_(1) = 6` and
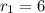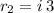`r_(2) = i\,3` and assume that
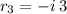`r_(3) = -i\,3`, the resulting polynomial is:

`p_(3) (x) = (x-6)\cdot (x+i\,3)\cdot (x-i\,3)`

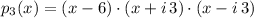
And by Algebra of real numbers we obtain the polynomial in its standard form:

`p_(3)(x) = (x-6)\cdot (x^(2)+9)`

`p_(3)(x) = x\cdot (x^(2)+9)-6\cdot (x^(2)+9)`

`p_(3)(x) = x^(3)+9\cdot x -6\cdot x^(2)-54`

`p_(3)(x) = x^(3)-6\cdot x^(2)+9\cdot x -54`

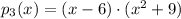
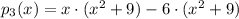
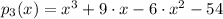
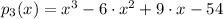
A polynomial function of degree 3 with real coefficients and the numbers 6 and i 3 as some of its zeroes is
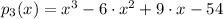`p_(3)(x) = x^(3)-6\cdot x^(2)+9\cdot x -54`.