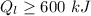Answer:
The value is
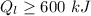
Step-by-step explanation:
From the question we are told that
The temperature of hot is
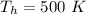
The temperature of cold is

The energy received is

Generally the maximum thermal efficiency of the engine is mathematically represented as
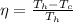
=>

=>
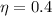
Generally the thermal efficiency of the engine is
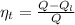
Here
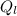 is the heat energy rejected
is the heat energy rejected
Generally the thermal efficiency must be less than or equal to the maximum thermal efficiency
So

=>

the change in inequality sign is because
 which was dividing started multiplying
which was dividing started multiplying
=>
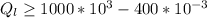
=>
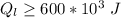
=>