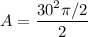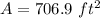A lawn sprinkler located at the corner of a yard is set to rotate through 90 degrees and project 30.0 feet. what area of lawn is watered by the sprinkler? round to the nearest w…

Question

asked Feb 28, 2021 162k views

1 Answer

Joel Handwell · Answer 1 · 2021-03-07T02:34:02+0000

Answer:

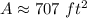
$A\approx 707 \ ft^2$

Explanation:

Area of a circular sector

A circular sector is defined by a central angle θ and the radius of the circle r. The area of the circular sector is:

$A={\frac {r^(2)\theta }{2}}$

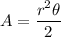
Note: θ must be expressed in radians.

The lawn sprinkler rotates θ=90° to an area of radius r=30 feet.

Expressing θ in radians:

$\theta=90*\pi/180=\pi/2$

The area is:

$A={\frac {30^(2)\pi/2 }{2}}$

$A=706.9\ ft^2$

$\boxed{A\approx 707 \ ft^2}$