Question

The sum of the age of two brothers is 22 years. Six years ago, the product of their ages was 21. Find the age of the elder brother.

Answer 1

The elder brother is 13 years old

Explanation:

System of equations

Let's set:

x=current age of the younger brother

y=current age of the elder brother

The first condition states the sum of their ages is 22:

x + y = 22

It follows that:

x = 22 - y

Their ages six years ago were: x-6 and y-6. The product of both is 21:

( x - 6 ) ( y - 6 ) = 21

Replacing the expression of x:

( 22 - y - 6 ) ( y - 6 ) = 21

Simplifying:

(16 - y ) ( y - 6 ) = 21

Multiplying:

`16y - 96 - y^2+6y=21`

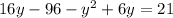
Rearranging and simplifying:

`y^2-22y+117=0`

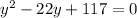
Applying the quadratic solver:

`\displaystyle y=(-b\pm √(b^2-4ac))/(2a)`

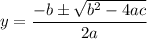
Where a=1, b=-22, c=117

`\displaystyle y=(22\pm √((-22)^2-4(1)(117)))/(2(1))`

`\displaystyle y=(22\pm √(16))/(2)`

`\displaystyle y=(22\pm 4)/(2)`

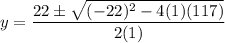
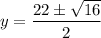
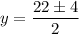
There are two possible solutions:

`\displaystyle y=(22+ 4)/(2)=13`

`\displaystyle y=(22- 4)/(2)=9`

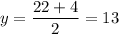
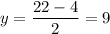
The value of x could have two solutions also:

x=22-13=9

x=22-9=13

Since y is the age of the elder brother, the answer is:

The elder brother is 13 years old