Question

In a recent survey of gun control laws, a random sample of 1000 women showed that 65% were in favor of stricter gun control laws. In a random sample of 1000 men, 60% favored stricter gun control laws. Construct a 95% confidence interval for p1 − p2.

Answer 1

`CI\approx\{0.0076,0.0924\}`

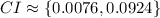
Explanation:

The formula for a z-confidence interval for a difference of proportions is
`\displaystyle CI=(\hat{p}_1-\hat{p}_2)\pm z^*\sqrt{\frac{\hat{p}_1(1-\hat{p}_1)}{n_1}+\frac{\hat{p}_2(1-\hat{p}_2)}{n_2}}`:

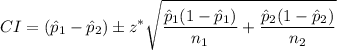Let
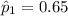`\hat{p}_1=0.65` to represent the sample proportion of
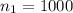`n_1=1000` women who are in favor of stricter gun control laws and let
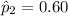`\hat{p}_2=0.60` to represent the sample proportion of
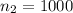`n_2=1000` men who are in favor of stricter gun control laws.

A 95% confidence level corresponds to a critical value of
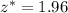`z^*=1.96`, so now we perform the necessary calculations assuming conditions are met:

`\displaystyle CI=(0.65-0.60)\pm 1.96\sqrt{(0.65(1-0.65))/(1000)+(0.60(1-0.60))/(1000)}\approx\{0.0076,0.0924\}`

Hence, we are 95% confident that the true difference in the proportion of women and men who favor stricter gun control laws is between 0.0076 and 0.0924

Since the interval does not contain "0" and only contain values greater than "0", it is more likely that the proportion of women who were in favor of stricter gun control laws is higher than the proportion of men who were in favor of stricter gun control laws.