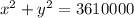Question

A university designs its campus with a master plan of two concentric circles. All of the academic buildings are within the inner circle (so that students can get between classes in less than 10 minutes), and the outer circle contains all the dormitories, the Greek park, cafeterias, the gymnasium, and intramural fields. Assuming the center of campus is the origin, write an equation for the outer circle if the diameter is 3800 feet. Equation Editor

Answer 1

`x^2+y^2=36100000`

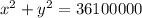
Explanation:

Here it is mentioned that the there are two concentric circles this means that they have the same center.

The center of the circles are the origin
`(0,0)`.

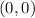Radius of the outer circle is

`r=(3800)/(2)=1900\ \text{m}`

Equation of a circle

`(x-a)^2+(y-a)^2=r^2`

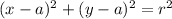
where

`a\ \text{and}\ b\ \text{are the}\ x\ \text{and}\ y\ \text{coordinates of the center}`

`r=\text{Radius of the circle}`

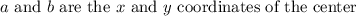
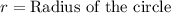
Here the equation will be

`(x-0)^2+(y-0)^2=1900^2\\\Rightarrow x^2+y^2=3610000`

The equation of the outer circle is
`x^2+y^2=3610000`