Consider the following cost function. A. Find the average cost and marginal cost functions. B. Determine the average and marginal cost when x = a. C. Interpret the values obtain…

Question

asked Jul 9, 2021 70.1k views

1 Answer

Alalalala · Answer 1 · 2021-07-15T21:17:10+0000

Answer:

a)Average cost function =
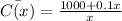
$\bar{C(x)}=(1000+0.1x)/(x)$

Marginal cost function =
C'x=0.1

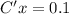
b)
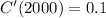
$\bar{C(2000)}=0.6$

C'(2000)=0.1

c)
$\bar{C(2000)}=0.6$ is the average cost to produce first 2000 items

C'(2000)=0.1 is the marginal cost to produce 2001 th item

Explanation:

Cost function:
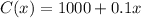
C(x) = 1000 + 0.1x

a)Find the average cost and marginal cost functions.

Average cost function =
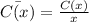
$\bar{C(x)}=(C(x))/(x)$

Average cost function =
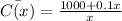
$\bar{C(x)}=(1000+0.1x)/(x)$

Marginal cost function =
C'x=0.1

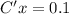
b) Determine the average and marginal cost when x = a.

a = 2000

Average cost function =
$\bar{C(x)}=(1000+0.1x)/(x)=(1000+0.1a)/(a)=(1000+0.1(2000))/(2000)=0.6$

So,
$\bar{C(2000)}=0.6$

Marginal cost function =
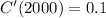
C'(2000)=0.1

c)Interpret the values obtained in part (b).

$\bar{C(2000)}=0.6$ is the average cost to produce first 2000 items

C'(2000)=0.1 is the marginal cost to produce 2001 th item