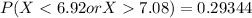Complete Question
Problem 7.43
A chemical plant superintendent orders a process readjustment (namely shutdown and setting change) whenever the pH of the final product falls below 6.92 or above 7.08. The sample pH is normally distributed with unknown mu and standard deviation 0.08. Determine the probability:
(a)
of readjusting (that is, the probability that the measurement is not in the acceptable region) when the process is operating as intended and
 = 7.0 probability
= 7.0 probability
(b)
of readjusting (that is, the probability that the measurement is not in the acceptable region) when the process is slightly off target, namely the mean pH is
 = 7.02
= 7.02
Answer:
a
The value is

b
The value is
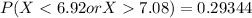
Explanation:
From the question we are told that
The mean is
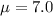
The standard deviation is
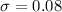
Considering question a
Generally the probability of readjusting when the process is operating as intended and mu 7.0 is mathematically represented as

=>
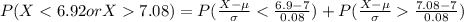
Generally
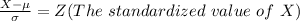
So
=>

=>
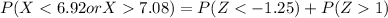
From the z table the probability of (Z < -1.25) and (Z > 1 ) is

and

So
=>
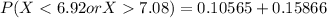
=>

Considering question b
Generally the probability of readjusting when the process is operating as intended and mu 7.02 is mathematically represented as

=>
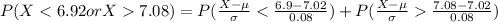
Generally
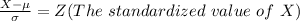
So
=>
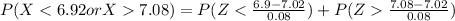
=>
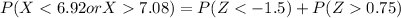
From the z table the probability of (Z < -1.5) and (Z > 0.75 ) is

and

So
=>
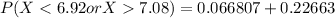
=>